Tajemství dvanáctistěnu

Pravidelný dvanáctistěn - pravidelný dodekaedr - zemský dvanáctistěn - vesmírný dodekahedron

---

Dvanáctistěn a Platón (mnohostěny - symboly 5 živlů)
Pět Platónových těles
Dvanáctistěn je pravidelný mnohostěn. Pravidelné mnohostěny se skládají z pravidelných mnohoúhelníků.Pravidelný
mnohoúhelník má všechny strany stejně dlouhé a všechny úhly stejně velké. Lze mu opsat i vepsat kružnici.
Obdobou pravidelných mnohoúhelníků v rovině jsou v prostoru pravidelné mnohostěny. Pravidelný mnohostěn
je takový mnohostěn, jehož všechny stěny jsou shodné pravidelné n-úhelníky, a v každém jeho vrcholu se stýká
stejný počet hran.

Připomeňme si také, že pro každé celé číslo n3 existuje pravidelný n-úhelník. Jistě by bylo možné předpokládat, že
obdobně pro každé celé číslo n4 by měl existovat pravidelný n-stěn. Ale není tomu tak. Pravidelných (platónslých)
mnohostěnů, samozřejmě pokud máme na zřeteli jen jejich tvar a nikoliv velikost, známe pouze pět. Které to jsou,
vyplývá z tabulky č. 1 (viz níže).

Zajímavé je, že těchto pět pravidelných mnohostěnů znali již starořečtí matematici počátkem 4.století př.n.l. Řecký
filozof Platón (427-347 př.n.l.) jich dokonce používal k objasňování svého učení o podstatě hmotného světa tím,
že krychli, osmistěn, čtyřstěn a dvacetistěn považoval za představitele čtyř základních živlů, jimiž byly podle jeho
učení země, vzduch, oheň a voda, a dvanáctistěn za představitele jsoucna neboli všeho, co existuje.
(podle Jirovské)

Dvanáctistěn a Kepler (konstrukce kulových ploch planetárních drah)
Pět platónských těles

Podobně bychom mohli rozvést i učení známého hvězdáře Johanna Keplera (1571-1630), podle něhož se tehdy šest
známých planet pohybovalo okolo Slunce po kulových plochách vepsaných nebo opsaných pravidelným
mnohostěnům. Například Země obíhá po kulové ploše procházející středy stěn pravidelného dvanáctistěnu (vepsaná
kulová plocha) a Mars po kulové ploše procházející vrcholy pravidelného dvanáctistěnu (opsaná kulová plocha). Tuto
Keplerovu teorii rozbil fakt, že vzájemná vzdálenost kulových ploch neodpovídala skutečným vzdálenostem planet
od Slunce. Kromě toho známe dnes další tři planety: Uran, Neptun a Pluto.

V roku 1597 sa Kepler oženil s Barbarou Müllerovou. V tom istom roku publikoval svoje prvé dielo, Mysterium
Cosmographicum, v ktorom argumentoval, že vzdialonosti medzi planétami boli určené podľa toho, ako sú vnorené
do piatich telies.

Keplerova konštrukcia - model, ktorým vysvetľuje vzdialenosti planét od Slnka - dosiahla prekvapujúco presné
výsledky, len s výnimkou Merkúra. Keplerov matematický talent predvedený v tejto knihe nezostal nepovšimnutý,
Tycho de Brahe ho pozval do Prahy, aby sa stal jeho asistentom a vypočítal nové orbity podľa Tychových
pozorovaní. Kepler sa presťahoval do Prahy v roku 1600.

Kepler pracoval ako asistent Tycha de Braha, až do jeho smrti v roku 1601, potom sa stal Tychovým nástupcom
na poste Ríšskeho matematika, najdôležitejšieho v Európe. Zotrval na tomto poste až do odvolania Rudolfa II. v roku
1612.

Dvanáctistěn a Euler
Pět platónských těles

Jak je možné, že pravidelných mnohostěnů je právě pět? Není možné, že jsme tvary některých mnohostěnů zatím
neobjevili? Dokažme si, že tomu tak není. Pro pravidelné mnohostěny můžeme odvodit vztah, rovnici vycházející ze
souvislosti mezi počtem hran v jednom vrcholu a počtem hran jedné stěny, která má pouze pětřešení.

Nejjednodušší mnohostěn má roh tvořený třemi rovnostrannými trojúhelníky, další jich mají čtyři nebo pět. Šest
rovnostranných trojúhelníků s jedním společným vrcholem poskládáme do roviny, takže nemohou tvořit povrch
mnohostěnu. Stejné to bude, když spojíme čtyři čtverce. Podobně tři pravidelné pětiúhelníky v jednom vrcholu jsou
maximum. Šestiúhelníky a mnohoúhelníky s více než šesti stranami jsou také vyloučeny.

V 18.století formuloval Leonard Euler (1707-1783) vztah pro každý konvexní mnohostěn. Byl to empirický objev
získaný pozorováním a matematicky dokázaný.

Dvanáctistěn a Morozov (zemský dvanáctistěn)
Reliktní tvar zeměkoule a jejích aktivních zón

V. Morozov, V. Makarov a N. Gončarov a další autoři přišli s teorií podle které lze zeměkouli účelně rozdělit
na dvanáctistěn složený z dvanácti pětiúhelníků. Středy vrcholových pětiúhelníků se překrývají s geomagnetickými
póly Země. Ostatní tvoří dva do sebe zapadající pásy po pěti pětiúhelnících okolo Země. V činnosti je také tzv.
reliktní dvanáctistěn, resp. jeho polární pětistěny, které jsou orientovány podle odlišného postavení zemské osy
v dávné minulosti. Podle částečných statistických odhadů mají středy pětiúhelníků, jejich strany, vrcholy a středy
stran mimořádné vlastnosti. Nacházejí se tu častěji naleziště surovin, existují tu častěji magnetické a gravitační
anomálie, dochází tu údajně k průniku s paralelními světy, k výronům energie, jsou tu silné geopatogenní zóny
(někdy tak silné, že jsou objektivně prokazatelné i bez speciálních přístrojů) atd. Následkem průniku
s paralelními světy dochází k přesunu nejrůznějších objektů, materiálů a souborů objektů. Při přesunech s návratem
dochází podle výpovědi zúčastněných často k efektu časového posunu.

Střed reliktního severního kruhu (přesněji řečeno pětiúhelníku) se nachází v sibiřském pohoří Putorana nedaleko
nejvyšší hory Kameň, která byla jedním ze sídel evenského boha ohně nazývaného různými evenskými kmeny
Agda, Agada, Ogul. Některé místní názvy v okolí hory mohou mít tibetský původ. Střed zmíněné kružnice leží
přibližně na sedmdesátém stupni severní šířky a devadesátém pátém stupni východní délky, v sevření řek Chet 
a Kotuj, u zálivu Chatanga.

Na linii B se nachází - Cheb, Pekelný vrch, Dolany u Plzně, brdský Plešivec, Blaník a Rudolec na Moravě,
kamenný obrázek u Laviček, Mostiště, Dolnomoravský úval.
Na linii C leží Česká Lípa,
Na linii D leží Ostrava (bod 1)
Linie K - prochází Blaníkem a zde protíná zde reliktní kružnici. 
Probíhá v Evropě na 49. stupni a 38. minutě sev. šířky (podle prof. 
Ramona)
(Podle Hrušky)

Dvanáctistěn a Jirovská (symetrie, Etruskové, da Vinci, ptolemaiovci, Pacioli, Newton aj.)
Matematická stránka problému (pravidelný pětiúhelník)

(Ve své diplomové práci věnované zlatému řezu se Iveta Jirovská věnuje i mnohostěnům a pravidelným
mnohoúhelníkům, mezi jejichž prvky existují také příklady poměru zlatého řezu. Důležitá je i stať o pětiúhelníku, který
tvoří stavební jednotku dvanáctistěnu.)

Počet pravidelných mnohoúhelníků, které můžeme sestrojit v rovině, je neomezený. V trojrozměrném prostoru
je počet pravidelných konvexních mnohostěnů pět.

Pythagorovci, zajímající se o takové záležitosti, považovali dvanáctistěn za hodný neobyčejné úcty a pozornosti.
Za znak svého bratrstva si vybrali pěticípou hvězdu, tvořenou úhlopříčkami pravidelného pětiúhelníku, který tvoří
stěny již zmíněného dvanáctistěnu. Pětiúhelník je jediný mnohoúhelník, jenž má týž počet úhlopříček jako stran,
je nejnižším mnohoúhelníkem, jehož strany i úhlopříčky lze nakreslit jediným tahem.

S pětiúhelníkem se setkáváme také vždy, když si zavazujeme tkaničky. Bylo by to vidět, kdybychom měli ploché
tkaničky a uzel bychom zatáhli až do konce. Sledujte uvázání uzlu na proužku papíru. Sestrojíme přesný pětiúhelník,
na jehož průsvitu vidíme pěticípou hvězdu.

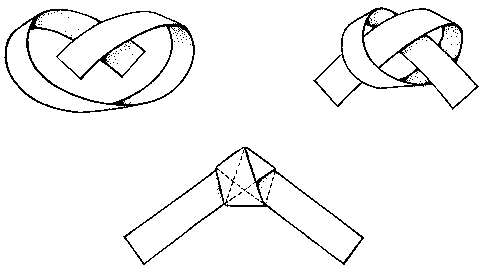
A jak sestrojíme pravidelný pětiúhelník pravítkem a kružítkem? Pokud známe poloměr kružnice opsané, můžeme
využít zlatého řezu. V kružnici se středem S zvolíme průměr AC a průměr BD na něj kolmý, bodem O rozpůlíme AS
a opíšeme z něj část kružnice o poloměru OD, která nám protne úsečku AC v bodě E. Vzdálenost DE je hledaná
velikost strany pravidelného pětiúhelníka. A nejenom to. Úsečka SE je stranou pravidelného desetiúhelníka.

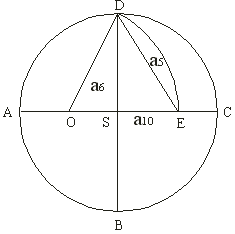
Již Eudoxos (4.st.př.n.l.) znal, že platí věta:

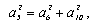
kde 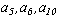značí strany pravidelného pětiúhelníka, šestiúhelníka a desetiúhelníka vepsaného témuž kruhu.
Pětiúhelník je bohatý zdroj zlatých poměrů. Snadno si ověříme následující vlastnosti.

1. Úhlopříčky v pravidelném pětiúhelníku se protínají v poměru zlatého řezu.

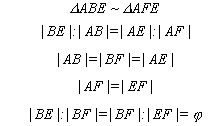
BF je větší díl úhlopříčky dělené zlatým řezem. Můžeme tedy sestrojit stranu pravidelného pětiúhelníku, je-li dána
úhlopříčka.

2. Poměr úhlopříčky a strany pravidelného pětiúhelníka je zlatý. Poměr 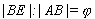vyplynul při odvozování
první vlastnosti.
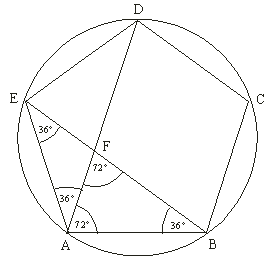
3. Jestliže sestrojíme všechny úhlopříčky tohoto pravidelného pětiúhelníku, dostaneme pěticípou hvězdu, uvnitř které
je opět pravidelný pětiúhelník.Platí, že průsečíky úhlopříček pravidelného pětiúhelníka ABCDE jsou vrcholy
pravidelného pětiúhelníka KLMNO. Poměr stran pětiúhelníků je roven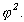

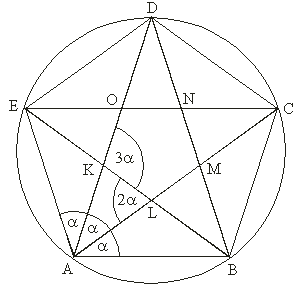
Podle věty o obvodovém úhlu dělí úhlopříčky každý vnitřní úhel pravidelného pětiúhelníka na tři shodné úhly.
Velikost každého z nich označme a = 36°. Z konstrukce je patrno

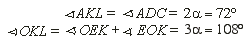
Pětiúhelník KLMNO je pravidelný. Označme délky jeho stran x. Je-li délka strany původního pětiúhelníka ABCDE
rovna jedné, platí:

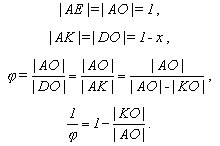
Úpravou a s použitím vlastnosti 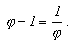dostaneme

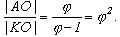
4.

Délky úseček KO, AK, AO, AD jsou členy geometrické posloupnosti:

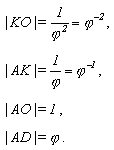
Součet dvou po sobě jdoucích členů se rovná následujícímu, např.

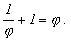
Pět Platónových těles

Pravidelný mnohoúhelník má všechny strany stejně dlouhé a všechny úhly stejně velké. Lze mu opsat i vepsat kružnici.
Obdobou pravidelných mnohoúhelníků v rovině jsou v prostoru pravidelné mnohostěny. Pravidelný mnohostěn je takový
mnohostěn, jehož všechny stěny jsou shodné pravidelné n-úhelníky, a v každém jeho vrcholu se stýká stejný počet m hran.

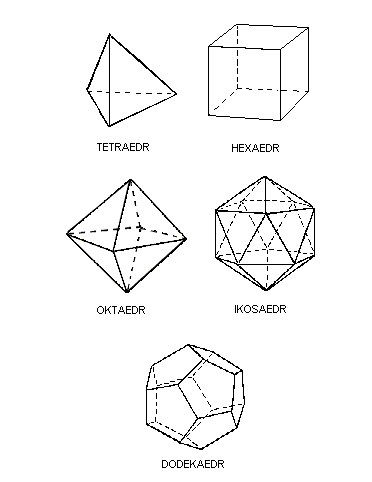
Připomeňme si také, že pro každé celé číslo n3 existuje pravidelný n-úhelník. Jistě by bylo možné předpokládat,
že obdobně pro každé celé číslo n4 by měl existovat pravidelný n-stěn. Ale není tomu tak. Pravidelných mnohostěnů,
samozřejmě pokud máme na zřeteli jen jejich tvar a nikoliv velikost, známe pouze pět. Které to jsou, vyplývá
z tabulky č. 1:

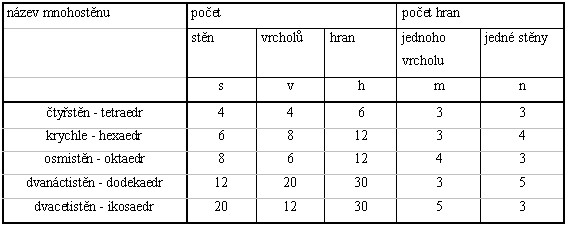
Zajímavé je, že těchto pět pravidelných mnohostěnů znali již starořečtí matematici počátkem 4.století př.n.l. Řecký
filozof Platón (427-347 př.n.l.)jich dokonce používal k objasňování svého učení o podstatě hmotného světa tím,
že krychli, osmistěn, čtyřstěn a dvacetistěn považoval za představitele čtyř základních živlů, jimiž byly podle
jeho učení země, vzduch, oheň a voda, a dvanáctistěn za představitele jsoucna neboli všeho, co existuje.
Podobně bychom mohli rozvést i učení známého hvězdáře Johanna Keplera (1571-1630), podle něhož se tehdy šest známých
planet pohybovalo okolo Slunce po kulových plochách vepsaných nebo opsaných pravidelným mnohostěnům. Například
Země obíhá po kulové ploše procházející středy stěn pravidelného dvanáctistěnu (vepsaná kulová plocha) a Mars
po kulové ploše procházející vrcholy pravidelného dvanáctistěnu (opsaná kulová plocha). Tuto Keplerovu teorii rozbil
fakt, že vzájemná vzdálenost kulových ploch neodpovídala skutečným vzdálenostem planet od Slunce. Kromě toho známe
dnes další tři planety: Uran, Neptun a Pluto.

Jak je možné, že pravidelných mnohostěnů je právě pět. Není možné, že jsme tvary některých mnohostěnů zatím
neobjevili? Dokažme si, že tomu tak není.
Pro pravidelné mnohostěny můžeme odvodit vztah

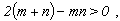
kde je počet hran jednoho vrcholu a n3 počet hran jedné stěny. Vyřešíme nerovnici pro všechna celá čísla m3 a n3.
Řešením jsou pouze hodnoty uvedené v tabulce o mnohostěnech.
Nejjednodušší mnohostěn má roh tvořený třemi rovnostrannými trojúhelníky, další jich mají čtyři nebo pět. Šest
rovnostranných trojúhelníků s jedním společným vrcholem poskládáme do roviny, takže nemohou tvořit povrch mnohostěnu.
Stejné to bude, když spojíme čtyři čtverce. Podobně tři pravidelné pětiúhelníky v jednom vrcholu jsou maximum.
Šestiúhelníky a mnohoúhelníky s více než šesti stranami jsou také vyloučeny.
V 18.století formuloval Leonard Euler (1707-1783) vztah pro každý konvexní mnohostěn:

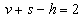
vztah mezi počtem vrcholů v, hran h a stěn s. Byl to empirický objev získaný pozorováním, kterému vyhovují i údaje
uvedené v naší tabulce pro pravidelné mnohostěny.
Jistě jste si v tabulce všimli této symetrie:

O krychli a osmistěnu říkáme, že jsou duální mnohostěny. Všimněte si, že středy stěn krychle jsou vrcholy pravidelného
osmistěnu a naopak středy stěn pravidelného osmistěnu jsou vrcholy krychle. Podobně jsou navzájem duální i pravidelný
dvanáctistěn a pravidelný dvacetistěn. Pravidelný čtyřstěn je duální sám se sebou.

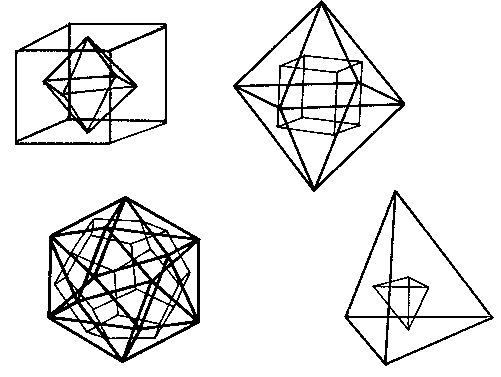
Zkusme uvažovat, proč byl právě dvanáctistěn oblíbenou hračkou etruských dětí před 2500 lety, jak ukázaly vykopávky
v Monte Loffa u Padovy. Pythagorejcům mohl být znám pravidelný osmistěn a dvanáctistěn - dvanáctistěn proto, že
v tomto tvaru krystalizují pyrity vyskytující se v Itálii a že s modely takových tvarů jako s ornamenty nebo
s magickými symboly se setkáváme právě u Etrusků.

Krychle a čtyřstěn také slouží lidem při jejich budovatelském úsilí i hráčských vášních. Dosvědčují to dětské
kostky i konstruktivistická architektura. Proč má hrací kostka z Ptolemaiovy doby vystavená v egyptologických
sbírkách Britského muzea právě tvar dvacetistěnu? Proč se od dávných dob až po naše časy užívají svítilny ve tvaru
pravidelného osmistěnu, i když jejich vnitřek prodělal vývoj od svíčky k výbojce?
Pěti pravidelným mnohostěnům se ve své knize "O božském poměru" věnuje i jeden z nejvýznamnějších
matematiků své doby Luca Pacioli (1445-1514). Kniha nazvaná podle "zlatého řezu" byla podle Vitruvia
věnována architektuře, pěti Platonovým tělesům a také proporcím lidského těla. Vyobrazení mnohostěnů na 59 tabulkách
pro svého přítele zhotovil Leonardo da Vinci, který si s oblibou vyráběl dřevěné kostry mnohostěnů.
Co božského našel na pěti jednoduchých tělesech Luca Pacioli, který žil více než dva tisíce let po Platonovi?
Je to jen ozvěna Platonova okřídleného rčení "Bůh činí vždy geometricky"? Nikoliv, mnich Luca Pacioli
myslil realističtěji: Bůh se jako geometr neprojevuje vždy, ale jen někdy. Zejména v případě tzv. zlatého řezu.
Pacioli zjistil, že je třináct projevů této božské proporce, a hledal je v nejdokonalejších matematických výtvorech,
pěti platonovských tělesech. Zhotovil je ze skleněných destiček a věnoval různým velmožům do jejich sbírek.
Kapitola "O dvanácté, téměř nadpřirozené vlastnosti" pojednává o pravidelném dvacetistěnu.
Podívejme se na tuto dávnou hrací kostku pozorněji. V každém vrcholu se stýká pět trojúhelníků a jejich třetí
strany tvoří pravidelný pětiúhelník. Spojíme-li dvě protilehlé hrany dvacetistěnu, dostaneme obdélník, který
také bezprostředně souvisí s božskou proporcí: Jeho delší strana je k menší ve stejném poměru jako součet stran
k delší.

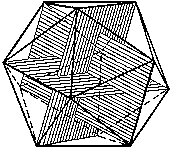
Dvanáct vrcholů dvacetistěnu tedy tvoří dvanáct vrcholů tří zlatých obdélníků, které leží ve třech navzájem kolmých
rovinách.

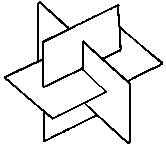
Jeho model tedy můžeme jednoduše udělat ze tří stejných čtvrtek papíru s poměrem stran j. Jejich společný průsečík
je střed dvacetistěnu. Hrany, které se protínají v jednom vrcholu tohoto tělesa, náleží pravidelnému pětibokému
jehlanu, jehož podstavu tvoří strany zlatého obdélníku, jehož delší strana je uhlopříčkou pravidelného pětiúhelníku
tvořícího podstavu jednoho z jehlanů.

Dvacetistěn souvisí s ještě jednou matematickou perličkou, problémem líbajících se koulí, který se stal předmětem
sporu Isaaca Newtona s oxfordským astronomem Davidem Gregorym.
Newton nedokázal Gregoryho přesvědčit, že maximální počet shodných koulí, které se všechny dotýkají jedné další
s nimi shodné koule, je nanejvýš třináct včetně koule líbané.

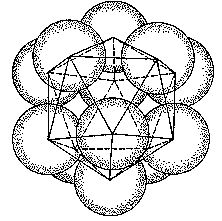
Škoda, že se tenkrát ještě nehrál pingpong, mohli si udělat pokus. Bez ohledu na pověry vzít třináct míčků a stáhnout
je průhlednou gumovou blánou. Přesvědčili by se, že dvanáct koulí se rozmístí do vrcholů pravidelného dvacetistěnu
a obklopí třináctou. Mezi nimi však zůstane trochu vůle. Je dost velká, aby se tam vmáčkla ještě čtrnáctá koule?
O to vlastně jde. Koule můžeme všelijak přeskupovat, ale pro čtrnáctou se místo neuvolní.

Ale i ostatní mnohostěny mají mnoho zajímavých vlastností:
Dvacetistěn může být vepsán do osmistěnu tak, že každý vrchol dvacetistěnu rozdělí hrany osmistěnu v poměru
zlatého řezu.
Vepíšeme-li do pravidelného dvanáctistěnu tři navzájem kolmé zlaté obdélníky, budou jejich vrcholy ležet
ve středech dvanácti pětiúhelníkových ploch.

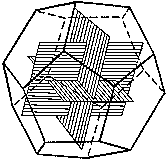
Estetické působení těchto těles nemůžeme ničím vysvětlit, avšak skutečnost, že tato tělesa byla užívána po celé generace
lidstva, je dostatečným důkazem.
(Diplomová práce; úryvek)

Dvanáctistěn a Hruška (zemský dvanáctistěn a anomální oblasti)
Paralelní svět

U nás se zabývá výzkumem zemského dvanáctistěnu pan Aleš Hruška ze Žďáru nad Sázavou a své poznatky
publikoval v knize Paralelní svět (vydavatelství Atelier, Žďár nad Sázavou). Rozvádí teorii o výskytu různých
anomálií a ložisk na klíčových bodech, hranách a dalších spojnicích zemského dvanáctistěnu. Zejména se zaměřuje
na posuny času, časoprostorové přesuny a paralelní prostor.

Dvanáctistěn a Nosreti (harmonické, morforezonanční a efektivní struktury)

Dvanáctistěn, dvacetistěn a šedesátistěn (úryvek)

Úkolem této úvahy je prostudovat matematické a geometrické 
vlastnosti zemského dvanáctistěnu, resp. jeho základního prvku - 
pětiúhelníku.

Nejprve si prostudujme obecnou otázku harmonických, morforezonančních a vůbec. tzv. efektivních tvarů a struktur.
O efektivní struktury se lidé nejčastěji zajímají v souvislosti s pyramidami a tzv. pyramidální energii. Proč jsou
některé tvary z hlediska vědou dosud ne zcela probádaného jevu morfické rezonance (konkrétně zde tzv. tvarové
energie) více efektivní než jiné? Pyramidální rezonance a tzv. pyramidální energie jsou samozřejmě jedním z případů
tvarové rezonance a "tvarové energie" a v ještě širším smyslu informačně-strukturální rezonance, tedy projevu obecného
formálního pole. Pojem energie dávám do uvozovek,protože i když některé aspekty působení tvarové rezonance
(např. při studiu CC) připomínají přesun energie (někdy jakoby pomocí vln šířících se kulovými vlnoplochami, jindy
jakoby přímým tečením potenciálu po nejkratší spojnici), jde spíše o působení energoinformační než energetické. Biolog
Rupert Sheldrak zjistil, že i biologické struktury a krystaly (tedy některé struktury fyzikální, resp. fyzikálně-systémové)
jsou schopné energoinformačního působení působení a nazval podstatu tohoto jevi morfickým, resp. morfogenetickým
polem. Tento termín rovněž charakteristicky odkazuje jak na aspekt strukturálně formální, tak na aspekt energetický
(pojem "pole"). Zdá se, že tvarová energie (pole) a morfogenetické pole jsou opět jen projevy všeobecného formálního
pole. Je zřejmé, že výzkum základního poznání se dnes již neobejde bez výzkumu formálního pole a jeho materiálních
a (jak se stále častěji ukazuje) i nemateriálních aspektů.

Vraťme se však k tzv. efektivním geometrickým tvarům a strukturám. Je zjevné, že energoinformačně aktivní struktury
jsou efektivními a harmonickými tvary i z mnoha běžných hledisek.

Můžeme tedy aplikovat různá hlediska efektivity a usuzovat z nich na přítomnost bioenergetické efektivity a souvislost
s ní. Obecná efektivita tvarů může být dobrým vodítkem při zkoumání morforezonančních (v biologii a medicíně
biorezonančních) struktur a při jejich teoretickém modelování.:

Prvním je hledisko "úspory materiálu", které je obdobou cesty nejmenšího odporu. - přírodní zákony často "donutí"
různé materiály/objekty, aby zaujaly "úspornou" strukturu. (U každého hlediska efektivity jde vlastně o spolupůsobení
"zákona" cesty nejmenšího odporu. Jde jen o to odhalit, jaké konkrétní síly a mechanismy toto působení
zprostředkovávají.) Pro solitérní objekty v ploše je "stavebně" nejúspornějším tvarem kruh, v prostoru koule.
Mnohoúhelník je tím úspornějším, čím má více stěn. V přírodě se mnohoúhelníky vyskytují málo, protože všeobecně 
existuje málo dvojrozměrných procesů/objektů (svět je přeci jen trojrozměrný). Přírodním příkladem kruhu je např. 
nasákavost papíru, vzniky "kruhů v obilí", růst některých hub v kruhu, šíření kruhů na vodě, šíření kulových vlnoploch
energií/emisí částic, šíření požáru atd. Většinou však nejde o zcela dvojrozměrné struktury, ale o trojrozměrné, které
se dvěma rozměrům z určitého hlediska jen velmi blíží. Někdy se ovšem přiblíží natolik, že v dané soustavě dochází
k anomálním efektům typickým pro 2D-soustavy. Příkladem jsou některé jevy v mikroelektrotechnice nebo jevy CC.

Můžeme se ptát i opačně. Proč některé anomální jevy vznikají na 2D-soustavách? Příčin může být více. Ale podstatnou
úlohu zde hraje fakt, že z hlediska strukturálního predstavuje 2D-vymezení v rámci 3D-prostoru velmi specificky
(výrazně) definovaný útvar, tekže u jakékoliv struktury v 2D-prostoru je větší předpoklad pro výraznější vliv
morforezonanční. Můžeme to trochu přirovnat k definičně vyhraněné ploše parabolické antény nebo anténním prvkům
uspořádaným v jedné rovině. Je jasné, že mezi nimi dojde snáze k souhře než mezi prvky a rezonančními/odrazovými
ploškami nacházejícími se na různých rovinách či dokonce rovinách nerovnoběžných. Z hlediska topologie 4D-prostoru
také pro 2D-systémy snáze nalezneme bod, ke kterému je z určitého místa "stejně daleko". 2D systém také může kopírovat
nějakou přirozenou hranici, například hladinu určitého elektrického potenciálu pole rostlin nebo rovinu styku určitých
materiálů. V tenké vrstvě také může být narušena 3-D logika krystalizace ve prospěch vlivu formálního pole.

Jako zvláštní případ 2D-soustavy můžeme chápat 1D-soustavy. Bylo zjištěno, že u velmi tenkých drátků dochází k emisi
studených elektronů. Je možné, že také tento jev souvisí s touto zvláštní topologickou strukturou.

Řada jevů v elektrotechnice vzniká na pomezi dvou materiálů, tedy vlastně v rámci 2D-soustavy. Výzkum formálního pole
(zde krystalického morfogenetického pole) může proto přinést revoluci i do této oblasti aplikované fyziky.

Pokud se tvary/objekty vyskytují v těsné blízkosti, pak kruh/koule není optimálním tvarem, nepředstavuje optimální
poměr mezi "obestavěným" prostorem a "spotřebovaným materiálem". Pokud bychom libovolně uspořádali
stejně velké kruhy nebo koule, vždy mezi nimi vznikne malý prostor s ostrými úhly, který bude mít extrémně nevýhodný
poměr mezi "obestavěným" prostorem a "spotřebovaným materiálem". V dvojrozměrné síti (a v síti,
kde je třetí rozměr z nějakého důvodu zanedbatelný) představuje optimální základní jednotku (modul) šestiúhelník.
Lidské technologie využívají šestiúhelník v tisícovkách aplikací, ale na mnoha místech (konkrétně např. ve stavebnictví)
je efektivita těchto a podobných struktur využívána málo. Zatímco ve dvojrozměrných síťových přírodních systémech
se zejména šestiúhelník vyskytuje často, v 3D-systémech jsou mnohostěny, a to zejména pravidelné, vzácné.

Přírodním příkladem. efektivního solitérního útvaru - koule - je např. kapka vody, ovocné plody, kulový blesk,
některé tvary UFO přírodního původu, šíření kulových vlnoploch světla, zvuku, exploze, jednoduché organizmy, tvar 
hvězd, planet atd.

Mnohostěny se v přírodě vyskytují zejména u krystalů, na jiných úrovních organizace hmoty jsou vzácnější. Proč?
Přírodě nestačí, že "ví", které tvary jsou efektivní. Musela by mít také více mechanismů, jak složité 3D-soustavy
konstruovat. Cesta nejmenšího odporu sama o sobě nestačí, přestože ve výsledku jsou tyto tvary skutečně v mnoha
ohledech efektivní a zákon nejmenšího odporu bezvýhradně dodržují (což vyplývá i ze studia CC).
 
Využití efektivních struktur je nepřeberné množství, přičemž zjevně vede šestiúhelníková síť aplikovaná často přírodou
i lidmi..Nejznámějším příkladem je asi stavba  včelích plástů, které jsou stavěny nad šestiúhelníkovou sítí. Relativně
efektivní přízemní dům s více místnostmi tedy můžeme s přivřením jednoho oka postavit na půdorysu šestiúhelníkové sítě
s tím, že vnější stěny, které již s dalšími stěnami nesousedí, mohou být vypuklé, sledovat tvar domu opsané, vepsané či
"kompromisní" koule.U takového domu by šlo relativně velmi výhodný poměr oběstavěného prostoru a použitého materiálu.
Malá plocha vnějších stěn má také vliv na úsporu tepla.

Ze stavebnictví přejděme k morforezonančním vlastnostem. Zkusme si představit, jak vzniká šesterečná souustava
u struktur CC. U malých vzdáleností atomárních sil je to jednoduché. Atomy se prostě usadí samy v síti nejmenšího
odporu a morfická rezonance se na tom podílí jen částečně. Na větších vzdálenostech (např. u CC-objektů) je takové
vysvětlení obtížnější. Koule vzniká jednodušeně vyrovnáním rovnoměrného tlaku působení jevu a tlaku okolí, resp.
ohraničením působnosti nějakého jevu, a kruh vzniká podobně stejně nebo je průmětem koule do 2D-roviny. Je zřejmé,
že žádný morforezonanční kruh není stejně aktivní na celém svém obvodu. Nyní si přibližme jeden ze způsobů, jak
může vzniknout další efektivní struktura - struktura šestiúhelníku (a další struktury šesterečné soustavy, např. kolo se
šesti loukotěmi). Stačí aby v jediném bodě obvodu morforezonančně vznikajícího kruhu vznikla určitá nestabilita
a toto místo se stane středem šíření dalšího kruhu, dalšího vlivu, který se sčítá s vlivem prvotním. Při studiu působících
sil snadno zjistíme, že nejstabilnější působení bude mít takový sekundární kruh, který bude mít shodný poloměr
s primárním. Takový kruh vytne na primárním kruhu další dva body, které jako součtové se stanou dalšími výraznými
šiřiteli vzruchu stejné vlnové délky, a navíc protne i střed, tedy posílí prvotní impuls. Tyto terciální body se již mohou
opřít o větší množství bodu rezonujících na stejné vlnové délce, takže dokončení celé šesterečné hvězdice je již snazší.

Podobně bychom odvodily i další CC-struktury a jejich prvky, do hry ale vstupuje i fraktální logika (která nesmírně
obohacuje tvarové možnosti), logika harmonických poměrů a logika kvantových jevů (které zodpovídají za "zaokrouhlení",
"zalomení" a "předzhotovení" struktur). Ve světě běžných energií se setkáváme spíše s jevem, že rezonují stejné délky
a jejich celočíselné násobky, příp. celočíselné podíly. Ve světě morfické rezonance však rezonují i další harmonické
násobky a podíly, například "délky", které se zvětšují/zmenšují podle konstantního čísla, přestože nemusí jít o číslo celé.
Nejvyšší morforezonanční stabilitu/účinek má zřejmě poměr zlatého řezu a mnohé přírodní jevy se o stabilitu tohoto
poměru přednostně opírají. Poměr zlatého řezu můžeme nalézt např. i v pravidelně se zvětšující (zmenšující ulitě hlemýždě.
Musíme si však uvědomit, že analogie šíření vlivu formálního pole se šířením energie po kulových vlnoplochách a
spojnicích bodů různého potenciálu jsou jen modelovými analogiemi, ve skutečnosti funguje mechanismus
morforezonance jinak. Některé obecné vlastnosti pole zde ale nacházíme. Díky existenci formálního pole s jeho
energoinformačním charakterem a nemateriálními aspekty dostává zpětně i pojem pole širší význam a jiš nikdy se
nebudeme moci podívat na jakékoliv fyzikální pole bez myšlenky, zda by nás k jeho poznání nepřiblížil nematerialistický
úhel pohledu stejně dobře jako ten tradičně materialistický a zda jeho dosah a působení není širší, než tradiční
jednostranně materialistická věda předpokládala.

Vidíme tedy přirozenou schopnost rezonance šesterečné soustavy a šestiúhelníku, resp. jemu opsaného kruhu - kola
se šesti rovnými nebo polokruhovými jednosměrnými nebo párovými loukotěmi. V šestiúhelníku má každá stěna
schopnost rezonovat s jinou stěnou a všechny dohromady zase s rozměrem vnitřní příčky - spojnicí každého vrcholu
se středem šestiúhelníku. Tato
vlastnost (vnitřní rezonance) má dva důležité efekty. Jednak usnadňuje informační výměnu (širší morforezonanční
¬ působení) v rámci reálných fyzikálních, biologických a kybernetických struktur (opora šesterečné antény), jednak
usnadňuje stabilitu a generování struktury a její další expanzi. Pro včelí architekty je určitě z více důvodů užitečné,
že tvar šestiúhelníku je tvarem ideálně rezonančním, ať už informaci o vznikající struktuře berou odkudkoliv.
Můžeme předpokládat, že skrze různé typy morforezonančních antén se přenáší (prostřednictvím formálního pole) nejen
informace o vlastní struktuře, ale různé přidružitelné informace, takže jde svým způsobem o obdobu antén pro
televizní či rozhlasové vysílání. V oblasti biologie (a nejen tam) a teorie informace je schopnost rezonance klíčovou
a biologické systémy se opírají o různé fraktální a jiné symetrické struktury, aby zvýšili své schopnosti rezonovat
prostřednictvím formální pole a přijatými/vyslanými informacemi zvyšovat stabilitu sebe či celého druhu.

Pokud u kruhů v obilí nalézáme často šesterečné loukotě, kruh dělený na šest dílů, kruh z šesti kruhů, šestiúhelník,
je to nepochybně proto, že takové struktury jsou nejefektivnější a rezonančně nejúčinnější. Tak je tomu i u mnoha
krystalů, sněhových vloček, ledových květů na skle atd. Vodní krystali mají pro výzkumníky formálního pole jednu
důležitou vlastnost: Zúčastněné atomy amolekuly nediktují krystalům nějakou aprirorní strukturu nějakými "oblíbenými"
vazebními úhly a délkami, takže tyto atomy a molekuly jsou z velké míry ovlivněny čistými "zájmy" formálního
pole. Tenké vrstvy mrznoucí vody jsou tak citlivým indikátorem lokálních projevů formálního pole. Někteří diagnostici
dokáží z ledových květů na skle usuzovat na přítomnost určitých látek v ovzduší či dokonce na onemocnění osob v místnosti.
Je možné, že jednou budou podobné metody nejen doménou senzibilů a jasnovidců, ale i automatizovaných diagnostických systémů.
Různé informace morfického pole mohou nést i krystalizační a sedimantační obrazce moči a krve, co je již dnes užíváno
k alternativní diagnostice.

Nyní se konečně dostáváme k otáze zemského dvanáctistěnu.

Nejprve je třeba vysvětlit, proč příroda použila právě 
pětiúhelníky, z nichž je zemský dvanáctistěn složen, když tvarem energeticky ("materiálově") nejúspornějším
a rezonančně nejefektivnějším je při výstavbě plošné sítě šestiúhelník. U struktur CC přichází na řadu pětiúhelník
a čtyřúhelník vždy, když jsou vrcholy šestiúhelníku z nějakého důvodu vytlačeny ze svých pozic. Představme si například,
že se prvotní morforezonanční kruh začne rozšiřovat. Definiční vliv se rozostří a opěrné body šesterečné soustavy
začnou být vytlačovány ze svých pozic, až zaujmou nové, semistabilní polohy.

Existuje i jiná možnost jak znázornit souvislost mezi šesti- a pětiúhelníkem. Pokud bychom chtěli relativně velký
šestiúhelník položit na kouli (např. na ideální zeměkouli), aby se k ní svou plochou co nejvíce přiblížil, museli bychom
ho nastřihnout a kousek založit, podobně, jako když chceme vyrobit z papírového kruhu kornout. Ze všech možností
prostorové redukce šestiúhelníku je právě pětiúhelník (tvořený pěti rovnostrannými trojúhelníky) z mnoha důvodů daleko
nejlepší (nejefektivnější, nejstabilnější). Pětiboká pyramida s rovnostrannými trojúhelníkovými stěnami stojí sice
na pětiúhelníkové základně, ale je vlastně "utajeným šestiúhelníkem", je morfickým rezonátorem šesterečné
soustavy (její stavební jednotka - rovnostranný trojúhelník - patří do šesterečné soustavy) představuje vlastně
šestiúhelník prostorově zakřiveným a do každé blízké roviny generuje morfické vlny (vlny formálního pole). Je třeba
si uvědomit, že trojúhelníky, na které můžeme rozdělit běžný pětiúhelník rovnostranné nejsou a jejich morforezonanční
a celkově "optimalizační" funkce je menší. Poněkud lépe je na tom trojúhelníky prostorově deformovaného
pětiúhelníku , promítnutého na povrch koule (tedy i pětiúhelníků zemského dvanáctistěnu), ale opravdu rovnostranné
jsou pouze trojúhelníky, jež vytvářejí boční stěny pětiboké pyramidy - jehlanu s pětiúhelníkovou základnou.

A nyní si představme souvislost zemského dvanáctistěnu a zemského šedesátistěnu. Zemský dvanáctistěn představuje
povrch Země rozdělen na 12 rovnostranných pětiúhelníků. Abychom znázornili příslušnost tohoto dvanáctistěnu do
šesterečné soustavy, musíme jej převést na šedesítistěn. Uděláme to jednoduše tak, že nad každým pětiúhelníkem
zkonstruujeme pětibokou pyramidu o stranách tvořených rovnostrannými trojúhelníky. Povrch (země)koule je tak
bezezbytku obsazen místo 12 pětiúhelníky 12 nízkými pětibokými pyramidami. Vznikl by vlastně vysoce symetrický
šedesátistěn tvořený 60 shodnými rovnostrannými trojúhelníky, rozdělenými do 12 pětibokých jehlanů. Je tu
zachována stejnost stran a stejnost úhlů jako u šestiúhelníku a navíc jde o prostorový útvar, prostorovou síť,
čímž se morforezonanční působení rozšiřuje o jednu dimenzi. Nad zemským dvanáctistěnem tak získáme další síť
pomyslných aktivních linií (tvořících šedesítistěn), které se na zemském povrchu příliš neprojevují, ale které
se mohou projevit při pokusech s modely. (Přestože je šedesátistěn vytvořen pomocí jediného typu stavebního dílku,
nejde o pravidelný mnohostěn, protože z různých vrcholů vychází různý počet hran.)

Pokud bychom si zhotovili malý model (zemského) šedesátistěnu, s údivem bychom zjistili, že povrch takového
rovnostranného (rovnohranného) šedesátistěnu můžeme vidět nejen jako sestavený z pětibokých pyramid nad pětiúhelníkovou
základnou, ale (a to více způsoby) z několika velkých šestiúhelníků (i když se jejich díly nenacházejí v jedné
rovině a netvoří povrch útvaru bezezbytku. Vždy zbude několik trojúhelníčků navíc, které jsou ovšem při jiném dělení
součástí zase jiného nerovinného šestiúhelníku. Všechny hrany celého šedesátistěnu jsou přísně "rezonanční"
a "materiálová" a "informační" (morforezonanční) efektivita struktury je teoreticky vysoká.

Komentář ke kosmickému dodekahedronu

Myslím si, že dnešní spekulace na téma uplatnění dodekaedru resp. dodekahedronu v kosmické architektuře
(viz následující články) nejsou tak úplně spekulacemi a přinejmenším jsou potvrzením správnosti mých úvah
o "efektivitě" těchto tvarů. Když i známý popularizátor vědy a zapřisáhlý odpůrce všech spekulací a vědeckého
šarlatánství Jiří Grygar říká, že to můžeme brát vážně, asi na tom něco bude. Máme příliš málo přijatelných
bezvadných modelů konstrukce vesmíru, než abychom mohli brát na lehkou váhu jakýkoliv model, který splňuje
základní požadavky na relativní úplnost a logickou bezchybnost. Takovému modelu pak musíme přiznat jakési
intelektuální prvenství, resp. aspoň pořadí v první desítce a dokud nebude objeven model lepší a realitě bližší,
musíme na něj pohlížet jako na ideu, která je v podstatě správná. Matematicka i fyzika znají mnoho podobných
příkladů modelů, o kterých již ani často nepřemýšlíme, zda jsou zcela reálné a pravdivé nebo ne, ale které nám
v podstatné nebo potřebné míře (relativně pravdivě) pomáhají chápat skutečné (pravdivé) souvislosti, jevy
a jejich aspekty. Takový model (teorii) pak považujeme za správný, a to až do chvíle než se objeví model vyšší,
který zpravidla zcela nezruší platnost staršího modelu, jen vyhovuje ve vice hlediscích a pro více případů a starý
model se stává jeho součástí, řešením pro určitý případ. V řadě případů také používáme pro určitý případ jeden
pohled (pojem, teorii) a pro jiný odlišný, přičemž víme, že každý má potřebnou míru pravdivosti. Žádná teorie
ani model stejně nejsou nikdy absolutně pravdivé, takže relativní pravdivost , bezchybnost a užitečnost jsou
často mírou zcela postačující.

Jde o to, že dosud nemáme přesvědčivý model vesmíru, který by splňoval základní předpoklady dialektického
myšlení, tedy, že by byl současně konečný a nekonečný. Dosud jsme při různých úvahách používali model
dokonalého (tedy kulatého) dvojrozměrného balónu. Jde o známý trik, jak si představit čtvrý rozměr, že jeden běžný
rozměr našeho prostoru vyloučíme a nahradíme čtvrtým rozměrem. Náš svět se tak splácne do roviny, na níž pak můžeme
pozorovat zakřivení ve vyšší dimenzi, v uvedeném případě do tvaru míče. Problém tvaru vesmíru tím ale není zcela vyřešen,
jen se vždy posouvá o jednu dimenzi výše. Jde o to, že také čtyřrozměrný vesmír musí být ukončen v rámci nějaké vyšší
dimenze atd. atd. Vesmír přitom nemůže mít příliš mnoho dimenzí, nebyl by stabilním a tak jak tak by v prvních vteřinách
jeho existence muselo dojít k redukci . Navíc reálný vesmír vždy při každé reálné experimentálně poznávací interakci)
zahrnuje nutně konečný počet dimenzí (každá poznávací interakce má schopnost odkrýt jen konečný počet dimenzí). Je to
podobně jako s cestou do nitra základních částic. Teoreticky mají nekonečnou (vrstevnatou) strukturu, díky níž jsou
nevyčerpatelné. A tak například proton obsahuje při postupných interakcích nekonečně mnoho protonů/vrstev. Důležité
ale je, že každá další vrstva je do jisté míry produktem další experminetální interakce, chcete-li: našeho pozorování.
Na hraniční mikro i makroúrovni je pozorovatel jakoby spolutvůrcem mikro- a makrokosmu a hranice mezi objektivním
a subjektivním mizí. (Z tohoto hlediska je i snazší připustit fakt, že vesmír je jen možností, kterou připustil Bůh, jeho
subjektivním pohledem.) Nekonečnost mikro- i makrodimenzí není absolutní, není zcela reálná a nelze je zcela oddelit
od hlediska a časoprostorového stanoviska pozorovatele. Zatímcovšak částice jsou potenciálně podrobovány interakcím,
vesmír nemá žádný pravděpodobný motiv zvyšování počtu reálných dimenzí/vrstev (vyjma myšleného vesmíru v našich modelech).
Vesmír tedy musí být nějakým způsobem zakřiven a ukončen sám v sobě při pohledu z kterékoliv reálné dimenze, a pro tyto
účely je model ideálního balónu příliš jednoduchý a již z hlediska pětirozměrného prostoru jde o neukončitelný tvar.
Přichází tedy model vesmíru v němž prostor tvoří jakási žebra po obvodu pětiúhelníků, z nichž je tvořen kosmický
dvanáctistěn. Model *** ovšemže představuje zase dimenzionální zjednodušení, takže vlastně nežijeme v prostoru
válců, ale v jejich plášti. Žijeme tedy ve stěně válce resp. (troj-, pěti-, šestibokého?) hranolu, jakéhosi potrubí (žebra),
z jehož kusů je svařen náš vesmír ve tvaru dedekaedru. Protože má místo hran "potrubí", říká se mu dodekahedron. Celý
vesmír je pak složen ze 120 těchto útvarů (dodekahedronů) těsně slepených v čtyřrozměrném prostoru do tzv.
Poincaréovy nadkoule. Samozřejmě, že nejde o 120 různých vesmírů, ale stále jen o náš jeden vesmír odrážející se
119-krát v zrcadlovém blidišty vícedimenzionálního prostoru (hyperprostoru). Pokud se tedy člověk vydá na konec vesmírného dodekahedru, vejde znovu do stejného vesmíru, ale z druhé strany.

Možná to ale autoři modelu dodekahedronu mysleli trochu jinak. Možná, že chtěli naznačit, že žijeme uvnitř dodekaedru,
ale tím, že ve svém modelu vytlačili hmotu do jeho pláště (redukce jednoho rozměru) a z pláště do hrany (redukce
dalšího rozměru) získali prostor pro znázornění zakřivení ve vyšším rozměru. Aby pozorovatelům nepřišlo divné,
že žijeme ve vesmíru rozměru linky, nafoukli ji do rozměru jakéhosi potrubí, ale ve skutečnosti jde možná o linku.
Snad se časem dozvíme podrobnosti. Všechna možná vysvětlení ale nic nemění na skutečnosti, že základním tvarem
od nějž je odvozena architektura vesmíru je dodekaedr.

K vesmírnému dodekahedronu musím uvést ještě jednu poznámu. Jak jsem již řekl, mírou správnosti modelu může být
i jeho užitečnost. A užitečnost nemusí být chápána jen z hlediska hrstky superodborníku, ale i širší intelektuální elity
nebo národa vůbec. Z tohoto hlediska se mi zdá nadkoule složená z dodekahedronů , i samotný dodekahedron zbytečně
složitým útvarem. Myslím, že nám docela postačí vědomí, že žijeme uvnitř dvanáctistěnu, jehož každé protilehlé strany
jsou (díky zakřivení vesmíru) totožné, takže dialektický požadavek jednoty konečnosti a nekonečnosti vesmíru je v tomto
modelu splněn. A tak možná stojíme na začátku nocé, pragmatické víry, víry o tom, že žijeme v dvanáctistěnu. Je to docela
sympatická a - podle matematiků a astronomů - i relativně pravdivá víra.


Dvanáctistěn a Luminet (vesmírný dedekahedron)
Vesmír jako míč? Důkazů je málo




Novou teorii, podle níž má kosmos "tvar fotbalového balonu", lze ověřit - už brzy se dozvíme, zda je, či
není správná


Náš zápas o určení tvaru a rozměrů vesmíru je sotva v poločase. Kosmos, který je malý, konečný a má tvar
"fotbalového míče" - takové tvrzení si žádá mimořádně přesvědčivé důkazy, a na ty si musíme počkat.

Ve čtvrtek 9. října uveřejnil nejprestižnější světový vědecký časopis Nature zhruba dvoustránkové sdělení čtyř
francouzských astrofyziků a jednoho amerického matematika o tom, že vesmír, v němž žijeme, je prostorově konečný
a poměrně malý - napříč měří jen něco přes 70 miliard světelných let. Tento překvapující závěr vzbudil nečekanou
pozornost našich i zahraničních sdělovacích prostředků patrně proto, že autoři doprovodili své sdělení kresbou
"tvaru vesmíru" v podobě fotbalového míče, sešitého z 12 rovnostranných pětiúhelníků. Dosud si většina
z nás nejspíš představovala vesmír jako kouli s nekonečným poloměrem.

Chcete-li publikovat v Nature, musíte napsat výjimečně dobrou a objevnou práci. Není tedy pochyb o tom, že zmíněné
sdělení pětice autorů pod vedením známého francouzského kosmologa Jean-Pierra Lumineta lze brát vážně, byť nám může
připadat bizarní - jenže taková je celá současná kosmologie. Autoři svou domněnku opírají o zatím nejkvalitnější
kosmologická pozorování drobných kolísání (fluktuací) teploty mikrovlnného záření kosmického pozadí (tzv. reliktního
záření), které uskutečňuje americká kosmická sonda WMAP (Wilkinson Microwave Anisotropy Probe).
Sonda nese jméno amerického kosmologa Davida Wilkinsona (1935 - 2002), jenž se významně podílel na výzkumu fluktuací
reliktního záření. Byla vypuštěna v létě 2001 a od října téhož roku je zakotvena v Lagrangeově bodě č. 2 soustavy
Slunce-Země, ve vzdálenosti 1,5 milionu kilometrů od Země (v Lagrangeových bodech se vyrovnává gravitační působení
Slunce a Země).

Příliš velké nástroje

V únoru 2003 zveřejnili američtí odborníci první výsledky dvou opakovaných přehlídek celé oblohy, jež sonda vykonala.
Tato zdaleka nejpřesnější data o stáří a struktuře vesmíru již posloužila ke zpřesnění našich znalostí o tom, jak
dlouho kosmos existuje: dnes s chybou pouhých dvou procent víme, že vesmír je stár 13,7 miliardy roků. Sonda také
odhalila skutečnost, že první hvězdy se objevily už 200 milionů let po velkém třesku.
Nyní tedy vyšla první práce, která využívá jemných efektů odhalených sondou k určení tvaru a velikosti vesmíru.
Nezůstane osamocená; další studie jiných výzkumných týmů, založené na týchž údajích ze sondy WMAP, budou zveřejněny
patrně ještě letos.
Mikrovlnné záření kosmického pozadí je fakticky nejstarší dochovanou zkamenělinou ve vesmíru poskytuje nám informace
o tom, jak vypadal kosmos asi 400 tisíc let po velkém třesku, kdy ještě neexistovaly žádné planety, hvězdy či galaxie
a vesmír sestával pouze ze dvou chemických prvků: vodíku a helia. Od té doby se vesmír podstatně zvětšil díky
pokračujícímu rozpínání prostoru, a tak je dnes vyplněn směsicí obdoby akustických vln nejrozmanitějších vlnových
délek. Kosmologové je mohou studovat právě prostřednictvím měření sondy WMAP, asi tak, jako lze rozborem zvukového
spektra hudební skladby určit, které nástroje v dané skladbě právě hrají.
Obecně pak platí, že vysoké tóny vyluzují nástroje menší, kdežto hluboké tóny nástroje velké. Luminetův tým zjistil,
že v kosmické kakofonii zcela chybějí hluboké tóny, tedy dlouhé vlnové délky.
To lze podle zmíněných autorů nejpřirozeněji vysvětlit tak, že ve vesmíru chybějí rozměrné "hudební nástroje"
prostě proto, že se do něho nevejdou. Jinými slovy, vesmír je konečný a astronomicky vzato poměrně malý: jeho průměr
činí v současnosti asi 70 miliard světelných let. (Dnešní astronomické přístroje dokáží pozorovat kosmické objekty
v kouli s poloměrem přibližně 12 miliard světelných let, v jejímž středu je Země.)

Těleso ve čtyřrozměrném nadprostoru

Ve zmíněné práci se pak autoři snaží dokázat, že pozorování učiněná sondou nejlépe odpovídají zvláštní geometrii
vesmíru, popsané modelem takzvané Poincaréovy nadkoule vnořené do čtyřrozměrného nadprostoru. (Francouzský matematik,
fyzik a filosof Henri Poincaré žil v letech 1854 až 1912 a je považován za Einsteinova předchůdce, pokud jde
o myšlenky obecné teorie relativity).
Nikdo z nás si neumí představit čtyřrozměrná tělesa, takže kvůli názornosti si pomáháme trojrozměrnými zjednodušeními
- to je právě ten dokonalý fotbalový míč sešitý z rovnostranných sférických pětiúhelníků, které bez mezer pokrývají
povrch obyčejné koule. Matematicky jde o pravidelný sférický dvanáctistěn a autoři se domnívají, že tvar vesmíru
lze popsat pomocí těsného "slepení" 120 takových dvanáctistěnů do Poincaréovy nadkoule, protože takový tvar
nejlépe odpovídá měřením družice WMAP.
Není však zdaleka jisté, že tento model bude vědeckou veřejností přijat. Má totiž důsledky, které lze ověřit nebo
vyvrátit pomocí astronomických pozorování. Podle předpovědi Luminetova týmu bychom měli pozorovat v datech o reliktním
záření z celé oblohy opakující se kruhové struktury o určitých úhlových rozměrech.
Právě o nalezení těchto struktur se pokouší už delší dobu skupina amerických kosmologů vedených Davidem Spergelem
z Princetonské univerzity, jenž se podílel na vývoji družice WMAP. I když jejich výsledky dosud nejsou zveřejněny,
podle předběžných údajů získaných na superpočítačích žádné očekávané kruhové struktury v datech družice WMAP Spergelovi
lidé nezjistili.
V tuto chvíli proto nemá mnoho smyslu spekulovat o tom, co by se stalo, kdyby další výzkumy Luminetovy názory potvrdily.
Ve vědě platí, že pro mimořádná tvrzení musí být sneseny mimořádně přesvědčivé důkazy, což se zatím pochopitelně
nestalo. Předností nové domněnky je však možnost ji ověřit či naopak vyvrátit rozborem nových astronomických měření.
Sonda WMAP dosud perfektně pracuje, což zvýší přesnost měření možná až dvojnásobně. Evropská kosmická agentura
připravuje na rok 2007 vypuštění ještě přesnější družice Planck, která by mohla přinést téměř jednoznačnou odpověď.
Ve fyzice jsme zvyklí brát nová data vážně, pokud výsledky pětkrát převyšují hodnotu chyb; z tohoto úhlu pohledu
je zápas o určení tvaru a rozměru vesmíru sotva v poločase.

Lidové noviny, 18. 10. 2003, Jiří Grygar
|Centrum částicové fyziky, Fyzikální ústav AV ČR, Praha


Přehledný vesmír

Byl bůh fotbalista? ptal se jistý německý týdeník v palcovém titulku. Nová teorie kosmologů vyvolala značnou
pozornost díky atraktivnímu balení - představě kosmu jako fotbalového míče. Také časopis Nature, ve kterém práce
vyšla, uveřejnil několik doprovodných textů, z nichž vyjímáme:

* Cesta napříč Luminetovým vesmírem by nás přivedla zpět do bodu, z něhož jsme vyšli. Neprošli bychom přitom žádnou
hranicí - podobně jako při plavbě kolem Země.

* Nejvzdálenější objekty by byly vidět v opačných směrech, jevily by se však různě staré. Pokoušet se nalézt touž
galaxii na dvou různých místech by bylo jako "snažit se rozpoznat stejnou osobu, vidíme-li ji zepředu ve věku 50
let a zezadu ve věku sedm let".

* Pouze v malém vesmíru, jako je ten Luminetův, můžeme spolehlivě předvídat budoucnost, třeba návrat Halleyovy komety.
Jen v kosmu, jehož velkou část přehlédneme, máme totiž přístup ke všem potřebným údajům.

Lidové noviny, 18. 10. 2003, ved

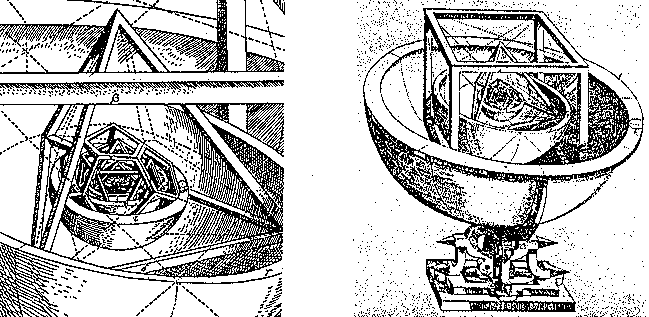
Podle francouzského kosmologa Lumineta (vpravo) se vesmír skládá ze 120 těchto útvarů
(dodekahedronů) těsně slepených do tzv. Poincaréovy nadkoule (kliknutím se obrázek zvětši)


Vesmír nemusí být jako míč

PRAHA - Ještě není jisté, zda má vesmír tvar fotbalového míče, míní český fyzik Petr Kulhánek k prohlášení
pěti francouzských a amerických vědců, že vesmír má zmiňovaný tvar. "Jde o jeden z mnoha navržených modelů,
který v tuto chvíli nejlépe odpovídá měřeným datům," potvrdil Kulhánek. Vědci však budou podle něj
k potvrzení modelu potřebovat týdny až měsíce. Podaří-li se jim to, půjde o nejvýznamnější okamžik moderní
kosmologie, řekl český odborník. Pětice vědců z Francie a USA, Jean-Pierre Luminet, Jeffrey R. Weeks, Alain
Riazuelo, Roland Lehoucq a Jean-Phillippe Uzan, zveřejnila minulý čtvrtek v renomovaném časopise Nature zprávu,
že výsledkům měření nejvíce odpovídá ze všech navrhovaných topologií konečný vesmír se strukturou založenou
na dodekahedronech (což je koule tvořená dvanácti pětibokými žebry). Podle tohoto modelu by měl být vesmír zakřiven
tak, že protilehlé hrany dodekahedronu jsou totožné, podobně jako na svinutém listu papíru jsou totožné slepené
okraje. Při pohledu vpřed podél papíru budeme vidět papír jakoby znova a znova. Podobně se nám bude vesmír jevit
jako složený z dodekahedronů, které na sebe donekonečna navazují. Nikdy v něm nenarazíme na žádnou hranici, i když
by byl ve skutečnosti konečný. Jeho základní stavební buňka - sférický dodekahedron - by mohla vzdáleně a zjednodušeně
připomínat fotbalový míč, vysvětlil český fyzik. Na počátku těchto úvah byl podle Kulhánka objev reliktního záření,
který učinili v roce 1965 Arno Penzias a Robert Wilson. Toto záření se oddělilo od hmoty 380 000 let po velkém
třesku a dnes v sobě nese informaci o tom, jak tehdy vesmír vypadal. Reliktní záření není ve všech směrech stejně
teplé, v některých nalezneme teplejší a v jiných chladnější skvrny. Rozdíl teplot je pouhá jedna stotisícina stupně.
Současná technika to ale dokáže rozlišit. Podle výsledků měření sondy WMAP, které byly zveřejněny letos 11. února,
je vesmír starý 13,7 miliardy let, je přibližně plochý a první hvězdy v něm vznikly po dvou stech miliónech let
od velkého třesku. Běžná hmota složená z atomů tvoří pouhá čtyři procenta hmoty vesmíru. Zbytek je skrytá energie
a skrytá hmota neznámé povahy.

http://pravo.newtonit.cz/default.asp?cache=229030


Vesmír jako míč? Důkazů je málo

to ostatní jsou spekulace, říká dr. Grygar


LN: Kdyby se "teorie kosmického míče" potvrdila, jak by se změnily naše představy o kosmu? Věděli bychom
například, jaká budoucnost vesmír čeká?

Podobně jako v historii, ani v astronomii nemá příliš mnoho smyslu spekulovat "co by, kdyby". Nová domněnka
je zatím příliš čerstvá a její vyhlídky tak nejisté, že by to byla doslova spekulace na druhou. I kdyby se nakrásně
Luminetova domněnka potvrdila, pochybuji, že by nám to pomohlo při odpovídání na otázku, jaká budoucnost vesmír čeká;
spíše by to takovou odpověď dále zkomplikovalo.

LN: Padly by teorie, podle nichž je náš vesmír jen jedním z mnoha existujících vesmírů?

Taková teorie ve skutečnosti dosud neexistuje. Spekulace o mnoha vesmírech je v nejlepším případě pracovní domněnkou
některých dostatečně odvážných kosmologů. Jedinou propracovanou kosmologickou teorií zůstává přirozeně pouze teorie
velkého třesku - to ostatní jsou vesměs jen tu nadějnější, tu beznadějnější spekulace.

LN: Pokud by byly Luminetovy představy správné, mohly bychom týž vzdálený objekt vidět na různých místech oblohy.
Bude v této souvislosti někdy možné zjistit, že dvě pozorované galaxie jsou vlastně jednou a toutéž galaxií?

V zásadě ano, ale při uvažovaném rozměru vesmíru, který má být přes 70 miliard světelných let, je téměř vyloučeno,
abychom ty další obrazy téže galaxie na různých místech oblohy spatřili. Opět opakuji, že zatím nemá mnoho smyslu
přemýšlet o důsledcích Luminetovy domněnky, když vůbec netušíme, zda přežije rok 2004.

---

Sestavil Darius Nosreti

Zkratky:

CC - zkratka pro tzv kruhy v obilí (nazývají se tak přestože se CC objevují i na jiných porostech a materiálech
a přestože mají strukturu většinou složitější než jen kruhovou)

Podklady:

Spirit 28 - 33/97
Aleš Hruška: Paralelní svět, Atelier, Žďár nad Sázavou
http://www.volny.cz/iveta.jirovska/diplomka4.html
http://aldebaran.feld.cvut.cz/vyuka/astrofyzika/gravitace/newton.html#Problems
http://pravo.newtonit.cz/default.asp?cache=229030
http://www.lidovky.cz
Poznámky:

.
- Dalsi zahady viz
http://www.pandora.cz/conference/ufo
Ilustrace:

Foto - in Lidové noviny, ostatní grafy, tabulka a symboly in Jirovská

---

100+1 zahraniční zajímavost 24/2002
věda a technika
SCIENCE & VIE, Paříž

HLEDÁNÍ
PARALELNÍCH SVĚTŮ

Kolik rozměrů má vlastně náš vesmír?
I když se to nezdá, všude okolo nás
mohou být jiné dimenze. Jsou tak ma-
lé,že si jich ani nevšimneme,nebo
naopak tak velké,že si je nikdy
nebudeme umět představit.


O třech rozměrech víme bezpečně od prvních
okamžiků našeho života; na čtvrtý, jímž je
čas, nás upozornily teprve v minulém století práce Hermanna
Minkowského a Alberta Einsteina.
Jenže je tu háček. Pohybovat se
třemi směry,zleva doprava,zdola nahoru či zezadu dopředu není
nic neobvyklého. Pohyb v čase
je však určen jen jedním směrem,
od minulosti k budoucnosti. Čtyř-
rozměrný časoprostor se tak sice
mírně vymyká našemu chápání,
ale právě díky němu se podařilo
popsat řadu jevů ve vesmíru.
Byl by omyl domnívat se, že
pochopíme-li pohyby galaxií, nic
nás nemůže na světě překvapit.
Zůstaneme-li na místě a sestoupíme-li do světa mikročástic, zjistíme, že zákonitosti ovládající vnitřek hmoty se nijak nepodobají ukázněnému oběhu planet ve
sluneční soustavě. Vysvětlení to-
hoto rozporu je možné. Jen musíme připustit, že vesmír má více
než jen čtyři rozměry.

VŠUDYPŘÍTOMNÉ
BUBLINY
Chceme-li přesně popsat polohu kteréhokoli místa na zemi či
určit rozměry nějakého tělesa, stačí nám k tomu tři údaje: výška,
šířka a délka. S jinými rozměry již
máme problém. Buď je můžeme
prostě ignorovat, nebo přistoupíme na tvrzení,že jsou tu, i když
je nijak nevnímáme. Již od dvacátých let minulého století uvažovali matematici Theodor Kaluza
a Oscar Klein o dalších rozměrech, které však jsou tak malé, že
naší pozornosti unikají. Jisté je jen,
že tyto rozměry navíc jsou zároveň rozměry konečnými ? jinak
by totiž nemohly být tak malé.
Jsou to zkrátka malé bubliny,
které je možné ?projít" a vrátit se
přitom na místo startu. Tyto rozměry jsou ve vesmíru všudypřítomné, tvrdí Brian Greene, jeden
z tvůrců tzv. teorie strun (viz
Vesmír plný strun 100+1 ZZ,
23/2001) a autor knihy Elegantní
vesmír. Znamená to, že jich je
nekonečně mnoho a nachází se
na každém místě našeho trojrozměrného vesmíru.

GRAVITACE JAKO
DŮKAZ
Jednou z nejpodivnějších sil ve
vesmíru je gravitace. Oproti jiným
silám je neobyčejně malá. Důkaz?
Magnet, který se vejde do kapsy,
dokáže ze země zvednout hřebík.
Je tedy schopen překonat svou
elektromagnetickou silou působení gravitace,kterou působí miliardy tun naší planety. Pro pochopení tohoto jevu je třeba opět
sáhnout ke skrytým rozměrům.
Představme si nyní dvojrozměrný vesmír ? třeba jako list papíru..
Bude tvořit jakousi membránu
(fyzikové jí říkají ?brána") a budou
v ní uloženy všechny galaxie. Nad
touto membránou je však ještě
další dimenze nebo i více dimenzí svinutých dohromady. A nyní dochází k zajímavému jevu. Zatímco elektromagnetická síla nebo
jaderné síly zůstávají uvnitř membrány, gravitace se bude šířit dále. Doslova se rozlije do okolních vesmírů a její hodnota se pro nás mnohonásobně zmenší. Tyto vesmíry pak podle poznatků moderní
fyziky nejsou od nás vzdálené
více než jeden mili-
metr ? a přesto se do
nich nikdy nedostane-
me.

POSKLÁDANÝ
VESMÍR
Dnes víme,že přes devadesát procent hmoty ve vesmíru uniká naší pozornosti. Známe sice její gravitační účinky,ale žádný teleskop ji dosud nedokázal zachytit. Proč? Mají-li pravdu američtí fyzici Steinhardt a Khoury, je to proto,že hvězdy se nacházejí jakoby ?za rohem ", neboli v jiném záhybu vesmíru. Podle jejich představy je vesmír
poskládán jako záclona. Světlo
hvězd v jiných záhybech se
musí šířit jen po své membráně
a do místa,kde se nacházíme,
proto nikdy nedorazí. Gravitace
však záhyby projde a podá svědectví o neviditelné vesmírné
hmotě. Tato hypotéza není sice
zdaleka jediným vysvětlením existence neviditelné hmoty, ale
mnoho vědců jí zcela propadlo.

ZROZENÍ Z OHNĚ
Membrány jsou zatím jen teoretickým pojmem. Připustíme-li však jejich existenci, dokážeme pomocí nich vysvětlit i takové
otázky, jako je vznik vesmíru, a to
zcela novým způsobem. Známý
Velký třesk, který stál na počátku
vesmíru, totiž podle Steinhardta,
Khouryho a dalších dvou vědců
nebyl ničím jiným než kolizí dvou
trojrozměrných membrán vznášejících se ve čtvrtém rozměru. Tyto membrány neobsahovaly
hmotu ? ta vznikla teprve při srážce. Výsledkem srážky byl vznik
našeho vesmíru a jeho galaxií,
který doprovází paralelní svět (pozůstatek druhé membrány nám
navždy nedostupný). Je dokonce
možné, že tento proces se v určitých periodách opakuje. Znovu
tak ožívá učení starověkých stoických filozofů,kteří předpokládali,
že po určité době vždy bude ves-
mír stráven ohněm a následně
vznikne vesmír nový. Jak je vidět,
přijít s něčím novým v oblasti pozná-
ní není až tak lehké. Je-li toto poznání pravdivé, bychom se mohli dozvědět již v nejbližších desetiletích..


Texty k obrázkům:
Náš vesmír je znázorněn jako plochá dvojrozměrná membrána. Milimetr nad ní se může nacházet další
rozměr,do kterého proniká pouze gravitace..


Další rozměry
Galaxie
Oslabená gravitace
našeho vesmíru
Gravitace šířící se
do dalších rozměrů
?Brána" neboli náš
vesmír


Další rozměry (několik
milimetrů)
Trojrozměrný vesmír
v podobě koule.V malém
měřítku tu existují další
svinuté rozměry.

Artistka se pohybuje po laně
vpřed a vzad. Lano je pro ni dvojrozměrným světem, protože jiným směrem se nebude moci
nikdy vydat. Oproti tomu mravenec lezoucí po laně si je vědom
dalšího rozměru, svinutého do
sebe, kterým je průměr lana.
Může po něm lézt dokola a žije
tak ve světě, který má o rozměr
více než svět artistky.


Gravitační vlny
Membrána našeho
vesmíru
Vzdálená galaxie
Dráha světla
Naše galaxie
Zhroucená hvězda
Složená membrána našeho vesmíru


Poskládaný vesmír
Světlo se šíří jen podél
jednotlivých membrán,takže není možné vidět
za záhyb. Gravitace galaxií však záhyby prochází a působí na nás.Tak by bylo možné vysvětlit,
proč nejsme schopni vidět velké množství
vesmírné hmoty.

Miliardy světelných let

Obr.: Vznik vesmíru kolizí membrán.
1 Membrány se k sobě přiblíží.
2 Velký třesk neboli
srážka dvou membrán.
3 Ze vzniklé hmoty
se utvoří galaxie.

---

Vědci vytvořili obraz vzniku vesmíru


WASHINGTON - Díky snímkům z družice WMAP se vědcům NASA podařilo vytvořit obraz mladého vesmíru. Obraz je tak detailní, že podle vědců pomůže najít odpovědi na nejdůležitější otázky týkající se vesmíru, zahrnující ...
Díky snímkům z družice WMAP se vědcům NASA podařilo vytvořit obraz mladého vesmíru. Obraz je tak detailní, že podle vědců pomůže najít odpovědi na nejdůležitější otázky týkající se vesmíru, zahrnující jeho vznik a pravděpodobný zánik. Astronomové na základě této mapky spočítali, že vesmír je starý 13,7 miliard let a hvězdy začaly zářit již 200 milionů let po tzv. velkém třesku. Shromažďování dat pro vytvoření tohoto obrazu trvalo rok. Družice WMAP kroužila ve vzdálenosti přibližně 1,6 milionu kilometrů od Země. WMAP (Wilkinson Microwave Anisotopy Probe, Wilkinsonova mikrovlnná anisotropní sonda) snímá období asi 380 tisíc let po velkém třesku - tedy dále, než je schopen Hubbleův teleskop na oběžné dráze kolem Země. Družice odeslala na Zem obraz oblohy jako pestrobarevného oválu. Horké oblasti jsou zachyceny žlutě a červeně, zatímco chladné modře a tyrkysově. V době po velkém třesku podle vědců neexistovaly hvězdy ani galaxie. Teplotní rozdíly byly jen malé. To postupně vedlo k tvorbě horkých a chladných oblastí signalizujících začátek koncentrace hmoty vedoucí ke struktuře nynějšího vesmíru. Z období velkého třesku se zachovaly stopy světla. Světlo, jež dnes zaznamenáváme jako mikrovlnné pozadí, k nám putovalo více než 13 miliard let, řekl vedoucí mise WMAP Charles Bennet. V tomto světle lze zaznamenat nekonečně malé rozdíly předznamenávající zárodky toho, co později přerostlo v chomáče galaxií a vesmír, který vidíme kolem sebe, dodal.

13.02.2003, mv, čtk

---

podrobne snimky kosmickeho mikrovln. pozadi


http://map.gsfc.nasa.gov/m_or.html

dalsi prehledy pribuznych URL-adres

http://www.altavista.com/web/results?q=WMAP+%22cosmic+microwave+background%22&pptt=WMAP%7Fcosmic+microwave+background&avkw=aapt&ppps=1

http://www.altavista.com/web/results?q=WMAP+%22early+universe%22&pptt=WMAP%7Fearly+universe&avkw=aapt&ppps=2

http://www.altavista.com/web/results?q=WMAP+%22first+year%22&pptt=WMAP%7Ffirst+year&avkw=aapt&ppps=3

http://www.altavista.com/web/results?q=WMAP+%22first+year%22+cosmology&pptt=WMAP%7Ffirst+year%7Fcosmology&avkw=aapt&ppps=7